电路理论

电路理论

《电路理论》课程包括：电路模型和电路定律、电阻电路的等效变换、电阻电路的一般分析、电路定理、动态电路分析、正弦电路分析、含耦合电感的电路、三相交流电路、非正弦周期电流电路、二端口网络、交直流电参数测量。

第 1 章：介绍和章节目标

本介绍性章节将作为对早期课程电路 I 和 II 中一些更重要主题的快速回顾。如果读者认为他或她对这些基本的电路分析和设计概念足够熟悉，可以跳过它。

完成本章后，您应该能够：

• 定义有源设备与无源设备
• 将 KVL 和 KCL 应用于电路
• 创建戴维宁和诺顿等效电路
• 在戴维南和诺顿等效电路之间转换
• 使用叠加定理分析多源电路

1.1 有源与无源设备：

有源器件是能够以电方式控制电流（电由电控制）的任何类型的组件。对于称为电子电路的电路，它必须至少包含一个有源器件。不能通过另一种电信号控制电流的元件称为无源器件。电阻器、电容器、电感器、变压器，甚至二极管都被认为是无源器件。无源器件可以具有线性电流与电压特性（如电阻器）或非线性 I 与V曲线（如二极管），并且通常是两个端子元件。有源器件包括但不限于真空管、晶体管、可控硅整流器 (SCR) 和 TRIAC。

所有有源设备都有控制电流通过它们的方法。一些有源器件允许电压控制该电流，而其他有源器件允许另一个电流作为控制信号。毫不奇怪，使用电压作为控制信号的设备被称为电压控制设备。以一种电流控制另一种电流的原理工作的器件称为电流控制器件。成功展示的第一种固态晶体管是电流控制器件。

1.2 符号和常规术语

这些页面中使用的电压和电流符号对应于以下约定： DC 偏置值由带有大写下标的大写字母表示，例如 V DS、I C。小信号变量的瞬时值由带有小写下标的小写字母表示，例如v gs , i d。总值由带大写下标的小写字母表示，例如 vBE、iD. 独立源的示意图符号为圆形，受控源的符号为菱形。电压源在符号内有一个±符号，电流源有一个箭头。原理图是按照标准惯例绘制的，其中最正的电源电压绘制在顶部，最负的电源电压绘制在底部。因此，正电流通常在原理图中从上到下流动。输入通常在左侧，输出在右侧，信号从左到右流动。

随着时间的推移，随着电子学研究的发展，某些术语的使用已经变得普遍或事实上的标准。一些术语和符号随着时间的推移在多种上下文中使用并具有不同的含义。其中一种情况是使用“饱和”一词。在双极结晶体管的上下文中，“饱和”的含义与场效应晶体管的上下文有很大不同。这可能会导致不熟悉电子产品的读者感到困惑。另一个例子是使用希腊字母 ? （测试版）。它用于表示运算放大器电路环境中的无量纲反馈因子以及 BJT 器件的无量纲电流增益。读者在阅读本文所涵盖的材料时应注意避免在遇到这些和其他此类上下文敏感术语时混淆。

在本文中，读者应该期望在各种示例电路中进行的计算应该产生合理的值。如果电源电压为 +/-10 V，则计算出的直流偏置值为 15 V（不在电源电压范围内）例如是不合理的。通常，偏置电流水平将在 1 微安到几百毫安之间。3.2 安培的计算偏置电流可能是不合理的，应该重新检查（除非可能是功率器件）。峰峰值交流电压应在电源电压范围内。应该重新检查不切实际的计算组件值。例如，电阻等于 0.013 欧姆。鉴于大多数电子元件的固有变化，三位有效数字足以表示结果。

1.3 基本数量。

描述电子系统运行的两个主要定律是欧姆定律和基尔霍夫定律。描述电子系统运行的主要量是电阻 R、电容 C 和电感 L。导数是电抗 X、阻抗 Z 和导纳，或全电导率 G。

假设读者对以下基本电路概念有一定程度的熟悉：

1. 欧姆定律
2. 无源电路分析
3. 基尔霍夫电路定律
4. 戴维宁和诺顿等效电路
5. 叠加定理
6. 受控来源
7. 理想的运算放大器
8. 变形金刚
9. 频率响应
10. 熟悉Spice电路模拟器或类似软件

下面是对其中一些概念的简短回顾。

1.4 基尔霍夫电路定律回顾

基尔霍夫电路定律是处理电路中电荷和能量守恒的两个等式，由 Gustav Kirchhoff 于 1845 年首次描述。这些“定律”广泛用于电子电路的分析和设计。

1.4.1 基尔霍夫电流定律（KCL）

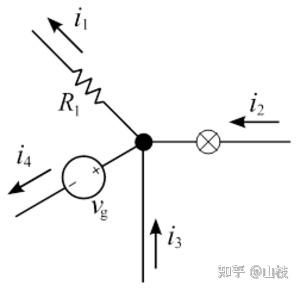
图 1.4.1 进入和离开节点的电流。

进入电路网络中任何结点的电流等于离开该结点的电流。

i 1 + i 4 = i 2 + i 3

该定律有时被称为基尔霍夫点规则、基尔霍夫结点规则（或节点规则）和基尔霍夫第一规则。

电荷守恒原理意味着：在电路中的任何节点（结）处，流入该节点的电流之和等于流出该节点的电流之和。否则，电荷会在节点上无休止地累积或排出，这在物理上是不可能的。

或者

导体网络中电流的代数和在一个点上相交为零。（假设进入结的电流为正，离开结的电流为负）。

回顾电流是一个有符号（正或负）量，反映朝向或远离节点的方向；这个原理可以表述为以下等式：

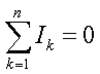
这里，n 是电流流向或远离节点的分支总数。该公式也适用于复杂电流：

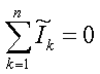
该定律基于电荷守恒，其中电荷（以库仑为单位）是电流（以安培为单位）和时间（以秒为单位）的乘积。基尔霍夫电流定律的矩阵版本是大多数电路仿真软件（如 SPICE）的基础。

1.4.2 基尔霍夫电压定律（KVL）

该定律有时称为基尔霍夫第二定律、基尔霍夫环（或网格）规则和基尔霍夫第二定律。

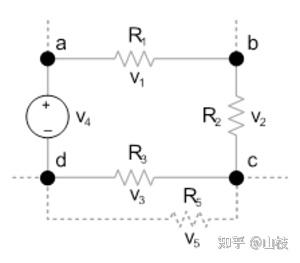
图 1.4.2 基尔霍夫电压定律

电路元件回路周围所有电压的总和为零。

v1 + v2 + v3 + v4 = 0

能量守恒原理意味着：

任何闭合电路周围的电势差（电压）的有向总和必须为零。

或者

简单地说，任何闭环中的电动势总和等于该环中电位降的总和。

或者

闭合回路中导体电阻与其中电流的乘积的代数和等于该回路中可用的总电动势。

与 KCL 类似，它可以表示为：

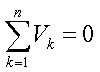
这里，n是测量的电压总数。电压也可能很复杂：

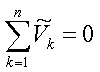
该定律基于“势场给予/获得的能量”的守恒（不包括耗散获得的能量）。给定电压电位，完成闭环的电荷在回到初始电位水平时不会获得或失去能量。

即使在电路中存在电阻（导致能量耗散）时，该定律也适用。如果人们意识到由于能量的耗散，电荷实际上不会回到其起点，则可以理解该定律在这种情况下的有效性。电荷只会终止在负极端子，而不是正极端子。这意味着电势差提供的所有能量（来自电源）已被电阻完全消耗，而电阻又会损失能量作为散热。

总而言之，基尔霍夫电压定律与电子元件（电阻器、电容器等）的能量增益或损耗无关。它是关于电压源产生的势场的定律。在这个势场中，无论存在什么电子元件，当电荷完成闭环时，“势场给出的能量”的增益或损失必须为零。

1.5 戴维南定理回顾

在电路理论中，线性电网的戴维南定理指出，电压源、电流源和两端电阻器的任何组合在电气上等效于单个电压源V和单个串联电阻器 R。对于单频交流系统，该定理还可以应用于一般阻抗，而不仅仅是电阻。

该定理指出，电压源和电阻器的电路可以转换为戴维南等效电路，这是电路分析中使用的一种简化技术。戴维宁等效电路可以用作电源或电池的良好模型（电阻代表内部阻抗，电源代表电动势）。该电路由一个与理想电阻串联的理想电压源组成。

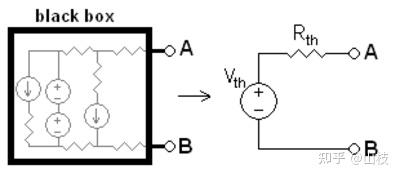
图 1.5.1 任何只包含电压源、电流源和其他电阻的黑匣子都可以转换为戴维南等效电路，恰好包含一个电压源和一个电阻。

1.6 诺顿定理回顾

线性电网的诺顿定理指出，任何具有两个端子的电压源、电流源和电阻器的集合在电气上等效于与单个电阻器 R 并联的理想电流源 I。对于单频交流系统，该定理也可以应用于一般阻抗，而不仅仅是电阻。Norton 等效项用于表示给定频率下的任何线性源和阻抗网络。该电路由一个与理想阻抗（或非电抗电路的电阻器）并联的理想电流源组成。

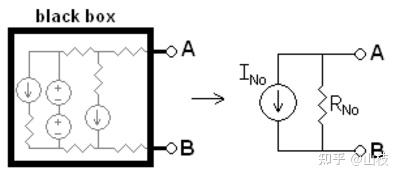
图 1.6.1 任何仅包含电压源、电流源和电阻器的黑匣子都可以转换为诺顿等效电路。

1.7 叠加定理回顾

叠加定理是天才的笔法之一，它采用了一个复杂的主题并以一种完全合理的方式将其简化。叠加定理中使用的策略是一次消除网络中除一个电源之外的所有电源，使用串联/并联分析来分别确定修改网络内每个电源的电压降（和/或电流）。然后，一旦为每个单独工作的电源确定了压降和/或电流，这些值就会全部“叠加”在彼此之上（以代数方式相加），以找出所有电源都处于活动状态时的实际压降/电流。为了理解这个概念，我们将分析以下示例电路并将叠加定理应用于它：

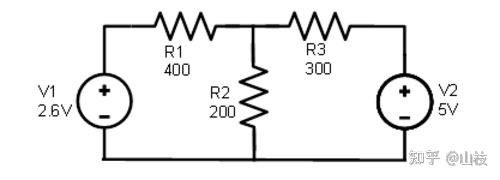
图 1.7.1

该电路中有两个电源，如图 1.7.1，因此我们必须计算两组电压降和/或电流值。一般规则，当将叠加定理应用于具有一个电源的串联/并联分析电路时，所有其他电压源都被短路取代，所有电流源都被开路取代。在这个示例电路中，我们只有电压源（电池）。在分析期间，每个非活动源都将被短路替换。

第一组是针对电路完成的，其中 5 伏电源被移除并替换为短路，仅剩下 2.6 伏电源，图 1.7.2。

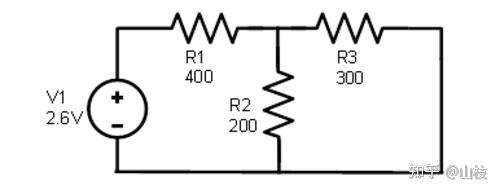
图 1.7.2

对于第二组，我们用短路替换 2.6 伏电源，只剩下 5 伏电源，图 1.7.3。

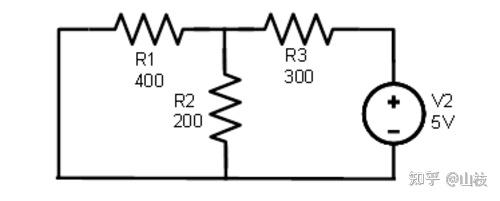
图 1.7.3

仅使用 2.6 伏电源分析电路，我们得到以下电压和电流值：

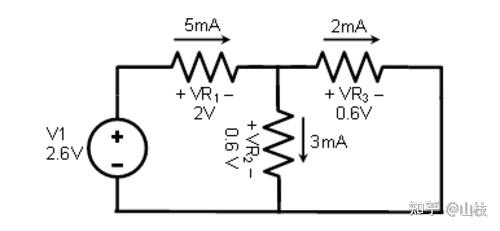
图 1.7.4

仅用 5 伏电池分析电路，我们得到另一组电压和电流值：

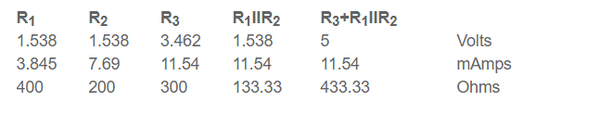
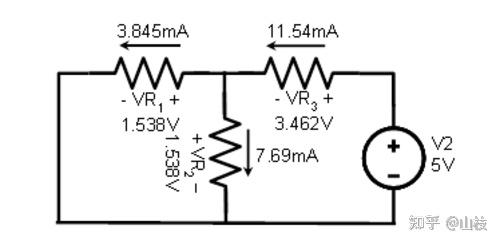
图 1.7.5

当叠加这些电压和电流值时，我们必须非常小心地考虑极性（电压降）和方向（电子流），因为这些值必须以代数方式相加。

将这些叠加电压应用于电路，最终结果如下所示：

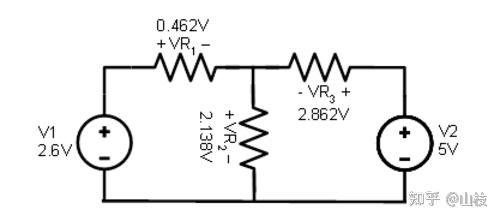
图 1.7.6

电流也以代数方式累加，并且可以像电阻电压降一样叠加，或者简单地根据最终电压降和各自的电阻 (I = V / R) 计算。不管怎样，答案都是一样的。这里我们展示了应用于电流的叠加方法：

再次将这些叠加的数字应用到我们的电路中：

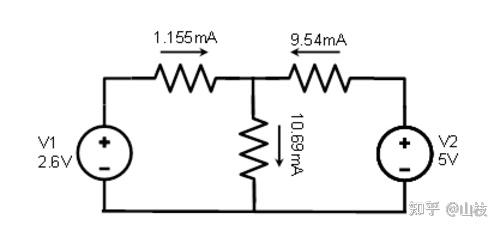
图 1.7.7

必须注意的是，叠加定理仅适用于每次可以将每个电源简化为串联/并联组合的电路（因此，该定理对于分析不平衡的桥式电路无用），并且仅适用于以下情况基本方程是线性的（没有数学幂或根）。线性的必要条件意味着叠加定理仅适用于确定电压和电流，而不适用于功率。功耗是一种非线性函数，当一次只计算一个源时，它不会通过代数计算得出准确的总数。对线性的需求也意味着该定理不能应用于元件电阻随电压或电流变化的电路中。因此，无法分析包含白炽灯泡等组件的网络。叠加定理的另一个先决条件是所有组件都必须是“双边的”，这意味着它们在电子流经任一方向时表现相同。电阻器没有极性特定的行为，因此我们迄今为止研究的电路都符合这个标准。所分析的电路中不能包括二极管等单向器件。

叠加定理可用于交流 (AC) 电路和半导体（放大器）电路的研究，其中有时交流经常与直流混合（叠加）。因为交流电压和电流方程（欧姆定律）就像直流一样是线性的，我们可以使用叠加来分析只有直流电源的电路，然后只有交流电源，结合结果来判断交流和交流会发生什么直流电源有效。不过，就目前而言，叠加足以打破必须通过联立方程来分析电路的情况。